CKKS学习心得

CKKS全过程

一些背景知识

分圆多项式

在复数集内有个单位根，分别是，其中，如果与互质，那么称为本原单位根。如下图的，，，。

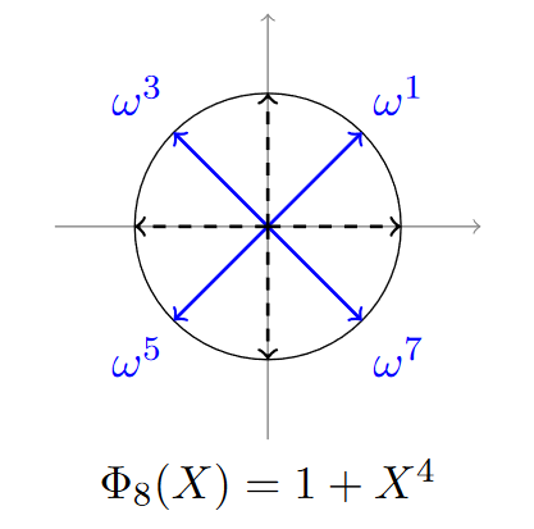
若一个整系数多项式的根都是n次本原单位根，这个多项式就是分圆多项式。它是一个不可约多项式，即：

如上图的。

性质：，即若，则

离散傅里叶变换：

傅里叶变换(FT)：对于函数，定义其傅里叶变换:

离散傅里叶变换(DFT)：对于个离散点序列，记，定义其DFT：

快速傅里叶变换(FFT)：对于以上DFT，将后面的和式分为偶数部分和奇数部分：

以上把一个规模为的DFT分解为个规模为的DFT，又，则；则有：

设，，对于多项式，令:

,

则有，若令，则有：

只需求出和，便可求出和，这样就把问题转化为一个递归问题，时间复杂度为。

现有：

根据其共轭性，可知的逆矩阵为，即

即可求得其系数。通过，时间复杂度为

CKKS的编码解码

两个算子：

：将复多项式解码为向量
假设是的整数次幂，明文，，分圆多项式的解为。
：；
：快速傅里叶逆变换，即通过求出。

：将缩减到。即设，：
，

注：如果我们在中编码向量时使用大小为的复数向量，我们需要通过复制其共轭根的来扩展出它的另一半。

编码解码：

编码：

1. 取
2. 用将扩展到
3. 计算，其中为精度控制。
4. 编码：

注：取整“”使用coordinate-wise random rounding(坐标随机舍入)，取正交基，令，。

解码：

以上算法可以看出，使用近似算法而不是精确算法。

加密解密

使用来编码和解码。取商环(通常是由中的所有多项式对不可约多项式 求模而形成的有限商（因子）环)。给定多项式对列表，搜索未知项式。其中：

• 是一组来自的随机已知多项式；

• 是一组环中关于界t的随机未知小多项式；

• 是环中关于界t的随机未知小多项式；

• =。

此处定义私钥是一对小多项式组，对应的公钥是一对多项式组，给定，，恢复多项式在计算上是不可实现的。

加密enc

设为编码后的明文多项式，设加密消息为，有：

其中是一组中关于界𝑡的随机小多项式，是系数为的多项式。

解密dec

计算：

中系数小的舍去，得到的结果乘以即可得到。

CKKS的同态运算(同态加和同态乘)

设为编码后的明文多项式，加密后为。

同态加：

1. 明文和密文加：

1. 密文和密文加：

同态乘：

1. 明文和密文乘：

1. 密文和密文乘：

其中，是一个小的随机多项式，是一个大整数，从中随机采样。的作用是将三维的密文调整为二维密文，同时可以进行计算。